IAY0340 - Exercise #14 - NAND model

Description of the task

During this lab you're going to model NAND gate in SPICE (Simulation Program with Integrated Circuit Emphasis) language. To do this we use eldorado simulator from Mentor Graphics. NAND model should be done for 180 nm technology such a way that positive slope and negative slope would be equal for the output signal. To achieve this you should change the width of the transistor. The length of the transistors must be 180 nm.

Using eldorado simulator

You should simulate your model in eldorado simulator from Mentor Graphics. In order to compile the files you need to:

• Write cad and choose Mentor Graphics (all will work exept QuestaSim (cad option b).
• Typing eldo [circuit name] compiles your model.
• To open a graphical representation of your model type ezwave and choose the corresponding compiler model. With right click on the plot you can add cursors, which would measure the signal values in time.

In order to practice using these tools a model of an inverter with wire connector to the inverter's output is given to you. On the Figure 1. is the schematic of the design.

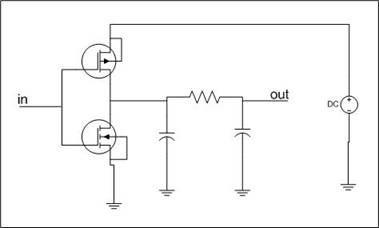
Figure 1. Schematic picture of the inverter with wire at the output.

Inverter model

For this model PMOS and NMOS transistors of 180 nm technology are used, therefore length of a transistor is 180 nm. However width is 2 times bigger and equals with 360 nm (the smallest possible). For wire model we have wire width of 2 * 180 nm = 360 nm. The length of the wire is 10 µm so we get resistance of 2,2 Ω and capacity of 2fF. The model written in SPICE is given to you in invWire.cir file. This model uses a subcircuit wire model which is given in wire.cir.

Firstly compile wire.cir and then invWire.cir. To use the subcircuit in your modules use the following SPICE syntax:
X[name] [connections] [name of subcircuit]
Also you need to include subcircuit file itself with: .INCLUDE [file name]

Hints for the solution

In order to find the ratio of width between NMOS and PMOS transistors they could be approximated as resistors. In this case R ~ µ^-1, where µ is mobility. For NMOS µ_n = 1250 cm²/V·s. For PMOS µ_p = 480 cm²/V·s. To find the correct ratio take the R ~ L/W as a reference. When taking account both mobility and size then R ~ L/(W·µ).

To describe MOS transistor in SPICE you need to declare it in the following format:
M[name] [drain node] [gate node] [source node] [bulk/substrate node] [model node] [model parameters (length L, width W)]

On Figure 2 is the schematic of the NAND.

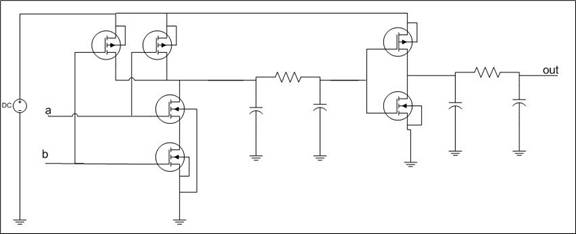
Figure 2. Schematic of the NAND.

Figure 3. Solution of the NAND.

Tasks

• Compile and simulate model of the inverter with wire at the output. Make sure the output is correct.
• Write the model of NAND gate with inverter on the output in SPICE, according to Figure 2. The skeleton of this model is given in nandInv.cir. To simulate the model we use pulses of 100MHz and reference voltage on 1,5V. Subcircuits of wire and inverter are given in separate files: wire.cir and inv.cir.
• Find appropriate width of PMOS and NMOS transistors in order to get the rising and falling edge time of output signal equal. The length of transistors should remain the same, 180 nm. Keep in mind that you can't make the width smaller than 360 nm. Slope time is defined as time when signal value is logically undefined - physical value being between 10% and 90% of reference voltage.
• Answer the questions.
• Write a report.

Questions

1. The NAND consists of NMOS and PMOS. What do the acronym mean?
2. If a design consists NMOS and PMOS transistors then how should it be called?