IAY0340 - Exercise #8 - FIR filter design and synthesis
Description of the task
Finite Impulse Response (FIR) filter is one of the most widespread numerical filters.
It is used practically everywhere in numerical signal processing including mobile
phones. The name of the filter comes from the fact, that single pulse passes
the filter within a finite amount of time. This time depends on the filter order:
it's the number of used coefficients. Testing of the filter is based on the
following feature - give a single pulse to the input and in finite amount of time
you must get all the filter coefficient values in the output.
You must design FIR filter with the order of nine, this means that design function
is data_out= ∑ ci * data_ini-1, where i=1, 2, ..., 9 and data_in-i
is delay for i cycles of input data_in.
In this lab everybody gets their own task, however a lot of basic solutions coincide.
Therefore teamwork is welcome. The difference of the tasks is in the values of
coefficients, which you can find according to your matriculation number rest of
division with 2, 3, 4, 5 and 7 gives you one of the coefficients according to the
table below. The filter is symmetrical (c1=c9), thus order of indexes
(incremental or decremental) is not important.
Table 1. Coefficients values
| Divisor -> |
3 |
4 |
7 |
5 |
2 |
| Rest |
c1, c9 |
c2, c8 |
c3, c7 |
c4, c6 |
c5 |
| 0 |
0,125 |
0,25 |
-0,75 |
1,25 |
1,0 |
| 1 |
-0,125 |
-0,25 |
0,75 |
-1,25 |
1,25 |
| 2 |
0,25 |
0,5 |
-0,625 |
0,75 |
|
| 3 |
|
-0,5 |
0,625 |
-0,75 |
|
| 4 |
|
|
0,875 |
0,875 |
|
| 5 |
|
|
-0,875 |
|
|
| 6 |
|
|
1,125 |
|
|
you can find a coeficient calculator
here. you have to just enter your student ID in the field.
Initial data
- 16 bit fixed point data: sign bit, 5 bits to the left side of the point, 10 bits to the right side of the point
- Filter's order is 9, coefficients could be found from the table above
- Entity is defined as following:
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_arith.all;
entity fir_filter is
port ( data_in: in signed (15 downto 0);
data_out: out signed (15 downto 0);
sample, clk: in bit );
end fir_filter;
- All calculations must be performed in 4 cycles (signal clk)
- Input and output of the data occur only if signal sample is true (not faster than every four cycle)
Hints
- To output real number in VHDL: debug_out<=real(conv_integer(data_out))/1024.0;
- 5 * a = 4 * a + a = (a << 2) + a;
- In division the round-up is not important.
- To test the behaviour a pulse with value 1.0 (040016) suits the best (see wave diagram below).
- 16-bit adder's approximate parameters:
| Name |
Area |
Delay |
| Small-slow |
124 |
19 ns |
| Quick-big |
570 |
5,9 ns |
- 16-bit multiplexer's approximate parameters:
| Name |
Area |
Delay |
| Small-slow |
2080 |
36 ns |
| Quick-big |
3860 |
21 ns |
Filter example
Try to understand the behavior of the filter by using the following
applet.
There are some
sample solutions of FIR on the RTL level. You can use them as a codebase
for your own.
Behavioral FIR filter simulation example
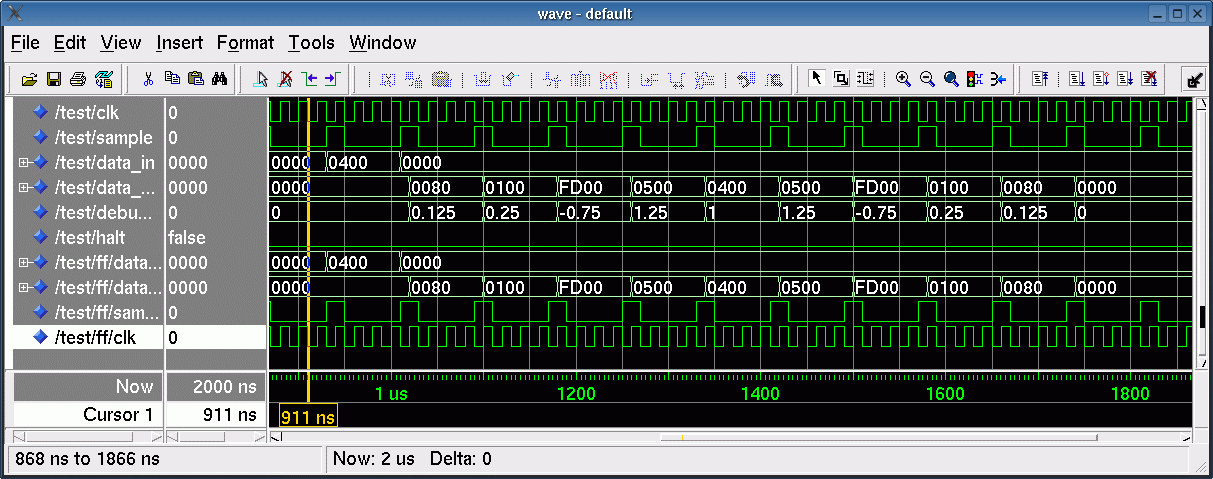
Figure 1. Sample of a simulation result of the behavioral design.
Tasks
- Create a behavioral module with your coefficients.
You can take the code FIR_beh.vhd as basis for your module.
This time you must write your own testbench.
Simulate and make sure that module works correctly (Figure 1).
- Choose architecture (use the simplest computational units as possible),
transform operations (if it is needed), schedule operations among cycles, create necessary
registers, bind operations to resources (your computational units). According to the results
of scheduling and binding write corresponding RTL code. The example of the RTL code
can be taken from RTL samples. Simulate your RTL code to check to correctness of the
behavior.
- Synthesize your FIR filter using Synopsis. Take a clock period of 20 ns. If it
is necessary change the code in order to get the smallest possible area (must be less than 3500).
- Write a report which contains:
- Behavioral, RTL and testbench code.
- Simulation results: behavioral and RTL.
- Made transformations: transformations of operations, scheduling and binding of operations.
- Synthesis results (area, delay, number of registers) and analysis. Especially
when delay 20 ns is not achieved.
Questions
- Why and where is FIR filters used?
- What is the main concept of FIR filters (how do they function)?
