Matriklinumber: 999999
Funktsioonide leidmine:
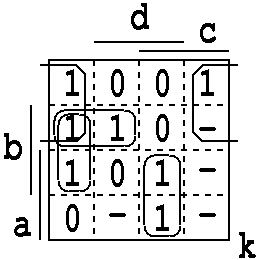
1. 5 : 2540BBCF : C6AE945 : 0,2,4,5,b,c,f / 6,9,a,e
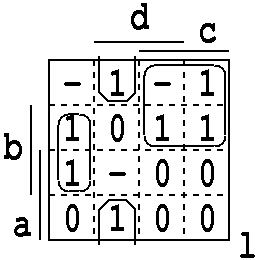
2. 7 : 1471C269 : 6D09623 : 1,2,4,6,7,9,c / 0,3,d
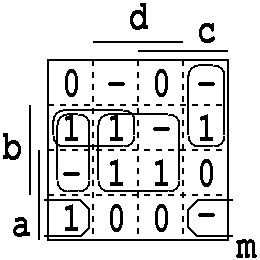
3. B : 4F556D8D : 1A71CF2F : 4,5,6,8,d,f / 1,2,7,a,c
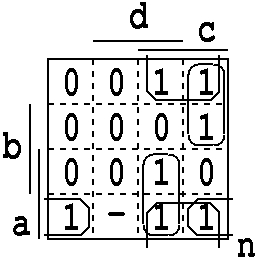
4. D : 82F386AB : 2BA68239 : 2,3,6,8,a,b,f / 9
| Lähte- ülesanne | espresso tulemus | espresso ver.2 (-Dexact) | Karnaugh kaart | Quine- McCluskey (pole vaja) |
0000 1-00 0001 01-0 0010 11-1 0011 0-01 0100 1110 0101 1010 0110 -111 0111 01-0 1000 0011 1001 -10- 1010 -0-1 1011 1001 1100 11-0 1101 0-10 1110 -000 1111 1011 |
-001 0100 -100 1100 1-11 1001 10-0 0011 010- 1010 -1-1 0010 0-10 0011 0-1- 0100 -01- 0001 0--0 1000 |
-001 0100 010- 1000 1-11 1001 10-0 0011 -1-1 0010 0-10 0011 0-1- 0100 -100 1110 -01- 0001 0--0 1000 |
0--0 1000 0-10 0011 0-1- 0100 -001 0100 1-11 1001 010- 1000 -100 1110 -1-1 0010 10-0 0011 -01- 0001 |
0--0 1100 0-10 1111 -001 0100 010- 1010 10-0 0011 -100 1110 -01- 0001 -1-1 0010 1-11 1001 0-1- 0100 |
Heuristiline lahendus (Karnaugh kaardid):




k = a' d' + a c d + a' b c' + b c' d'
l = a' c + b' c' d + b c' d'
m = a' c d' + b c' d' + b d + a b' d'
n = a' c d' + a c d + a b' d' + b' c
See tulemus langeb kokku espresso teise tulemusega.
Alternatiiv: m2 = a' c d' + a'b c' + bd + a b' d'
Näidiseks ka täpne lahendus Quine-McCluskey meetodiga. Lahenduskäik on siin.
Iga elemendi taga: [pindala/viide] andmete valmisoleku aeg (eeldusel, et sisendites on see 0).
ai = a' [1.5/1.5] 1.5 bi = b' [1.5/1.5] 1.5 ci = c' [1.5/1.5] 1.5 di = d' [1.5/1.5] 1.5 t0 = ai & di [2.0/2.0] 3.5 t1 = ai & c & di [2.5/2.5] 4.0 t2 = ai & c [2.0/2.0] 3.5 t3 = bi & ci & d [2.5/2.5] 4.0 t4 = a & c & d [2.5/2.5] 2.5 t5 = ai & b & ci [2.5/2.5] 4.0 t6 = b & ci & di [2.5/2.5] 4.0 t7 = b & d [2.0/2.0] 2.0 t8 = a & bi & di [2.5/2.5] 4.0 t9 = bi & c [2.0/2.0] 3.5 k1 = t0 + t4 [2.0/2.0] 5.5 k = k1 + t5 + t6 [2.5/2.5] 8.0 l = t2 + t3 + t6 [2.5/2.5] 6.5 m1 = t1 + t6 [2.0/2.0] 6.0 m = m1 + t7 + t8 [2.5/2.5] 8.5 n1 = t4 + t9 [2.0/2.0] 5.5 n = n1 + t1 + t8 [2.5/2.5] 8.0
k, m ja n tükeldamisel on üritatud tasakaalustada viidet.
Elemendid: 4 x NOT, 4 x 2-AND, 6 x 3-AND, 3 x 2-OR, 4 x 3-OR
Kokku: 21 elementi, suurus 45, kriitiline tee 8.5
k = a' d' + a c d + a' b c' + b c' d'
l = a' c + b' c' d + b c' d'
m = a' c d' + b c' d' + b d + a b' d'
( m2 = a' c d' + a' b c' + b d + a b' d' )
n = a' c d' + a c d + a b' d' + b' c
Ühised alamavaldised - ühised tuumad =
mittetriviaalsed, ühised konjunktsioonid = triviaalsed.
Tuumade leidmisel on näidatud ainult tuumadeni viivad
jagajad ja jagatised.
| k | tuumad | l | tuumad | m | tuumad | m2 | tuumad | n | tuumad |
/ a' / b c' / d' |
d' + b c' a' + d' a' + b c' |
/ c' |
b' d + b d' |
/ b / d' |
c' d' + d a' c + b c' + a b' |
/ a' |
c d' + b c' |
/ a / b' / c / d' |
c d + b' d' a d' + c a' d' + a d + b' a' c + a b' |
On näha, et m ja n kahel tuumal on mittetriviaalne ühisosa - (a'c+ab').
Lisaks võib teha järgmised järeldused:
1. k tuum (a'+d') on realiseeritav ühe 2-NAND
elemendiga;
2. l tuum (b'd+bd') on realiseeritav ühe 2-XOR
elemendiga;
3. m ja n tuumade ühisosa (a'c+ab') sisaldab
implikanti t2 (st. a'c);
4. m tuumast (a'c+bc'+ab') üle jääv osa
vastab jagajale, mis annab k tuuma (a'+d')
(st. bc');
5. n tuuma (a'd'+ad+b') üks osa on realiseeritav
2-XNOR (XOR+NOT) elemendiga (jääb antud juhul kasutamata).
Need on olulised, kui eesmärgiks on viia skeem nii väikseks kui võimalik. Tulemuseks on ka mõned ühised triviaalsed alamavaldised (lisaks lihtimplikantidele).
Jagamised on jäetud kirjelduse lühiduse huvides näitamata.
Parameetrite esialgne kasv pole midagi hullu, sest eeldatavasti kahandavad järgnevad teisendused (eriti DeMorgan) skeemi suurust oluliselt.
k = a' d' + a c d + ( b c' ) ( a' + d' )
l = a' c + ( c' ) ( b' d + b d' )
m = ( d' ) ( ( a' c + a b' ) + b c' ) + b d
n = ( d' ) ( a' c + a b' ) + a c d + b' c
ai = a' [1.5/1.5] 1.5 bi = b' [1.5/1.5] 1.5 ci = c' [1.5/1.5] 1.5 di = d' [1.5/1.5] 1.5 t0 = ai & di [2.0/2.0] 3.5 t2 = ai & c [2.0/2.0] 3.5 t4 = a & c & d [2.5/2.5] 2.5 t7 = b & d [2.0/2.0] 2.0 t9 = bi & c [2.0/2.0] 3.5 t50 = b & ci [2.0/2.0] 3.5 t51 = ai + di [2.0/2.0] 3.5 t52 = b [xor] d [2.0/2.0] 2.0 t53 = a & bi [2.0/2.0] 3.5 t54 = t2 + t53 [2.0/2.0] 5.5 t55 = t50 + t54 [2.0/2.0] 7.5 t1t6t8 = di & t55 [2.0/2.0] 9.5 t1t8 = di & t54 [2.0/2.0] 7.5 t3t6 = t52 & ci [2.0/2.0] 4.0 t5t6 = t50 & t51 [2.0/2.0] 5.5 k = t0 + t4 + t5t6 [2.5/2.5] 8.0 l = t2 + t3t6 [2.0/2.0] 6.0 m = t1t6t8 + t7 [2.0/2.0] 11.5 n = t1t8 + t4 + t9 [2.5/2.5] 10.0
Elemendid: 4 x NOT, 10 x 2-AND, 1 x 3-AND, 5 x 2-OR, 2 x 3-OR, 1 x 2-XOR
Kokku: 23 elementi, suurus 45.5, kriitiline tee 11.5
( b c' ) ei ole eraldi realiseeritud
k = a' d' + a c d + ( b c' ( a' + d' ) )
l = a' c + ( c' ) ( b' d + b d' )
m = ( d' ) ( a' c + a b' ) + b c' d' + b d
n = ( d' ) ( a' c + a b' ) + a c d + b' c
ai = a' [1.5/1.5] 1.5 bi = b' [1.5/1.5] 1.5 ci = c' [1.5/1.5] 1.5 di = d' [1.5/1.5] 1.5 t0 = ai & di [2.0/2.0] 3.5 t2 = ai & c [2.0/2.0] 3.5 t4 = a & c & d [2.5/2.5] 2.5 t6 = b & ci & di [2.5/2.5] 4.0 t7 = b & d [2.0/2.0] 2.0 t9 = bi & c [2.0/2.0] 3.5 t51 = ai + di [2.0/2.0] 3.5 t52 = b [xor] d [2.0/2.0] 2.0 t53 = a & bi [2.0/2.0] 3.5 t54 = t2 + t53 [2.0/2.0] 5.5 t1t8 = di & t54 [2.0/2.0] 7.5 t3t6 = t52 & ci [2.0/2.0] 4.0 t5t6 = t51 & b & ci [2.0/2.0] 5.5 k = t0 + t4 + t5t6 [2.5/2.5] 8.0 l = t2 + t3t6 [2.0/2.0] 6.0 m = t1t8 + t6 + t7 [2.5/2.5] 10.0 n = t1t8 + t4 + t9 [2.5/2.5] 10.0
Elemendid: 4 x NOT, 7 x 2-AND, 3 x 3-AND, 3 x 2-OR, 3 x 3-OR, 1 x 2-XOR
Kokku: 21 elementi, suurus 43, kriitiline tee 10.0
Kuna see variant on parem kõkide parameetrite alusel, siis sellega edasi jätkangi. Vajadusel saab ka siit variant #1-le vastava skeemi eraldada.
Eesmärgiks on lahti saadi kallitest elementidest - invertorid, AND ja OR elemendid. Ning NAND on parem kui NOR. Teisenduste alusteks on DeMorgani ja topelteituse seadused: ( x' + y' ) = ( x y )', ( x' y' ) = ( x + y )' ja ( x' )' = x.
Üldjoontes toimub teisendus selliselt, et nii AND kui ka OR elemendid
muudetakse NAND elementideks - x y + w z = ( ( x y )' ( w z )' )'.
Sisendmuutujate inverteerimisest lahti saamiseks sobivad järgmised
teisendused (otse- ja inverteeritud väärtuste kombinatsioonid):
a) x y z' = ( x y ) z' = ( ( x y )' + (z')' )' = ( ( x y )' + z )'
b) x y' z' = x ( y' z' ) = x ( y + z )'
c) x' y' z' = ( x + y + z)'
Teisendused on teostatud väljundite kaupa. Paaril korral on esitatud kaht alternatiivi koos võrdlusega.
==k==
t51 = ai + di ===> t51 = (a & d)' [1.0/1.0] 1.0
t5t6 = t51 & b & ci =1=> t5t6x = (t51 & b)' [1.0/1.0] 2.0
t5t6i = t5t6x + c [2.0/2.0] 4.0
ci = c' =2=> ci = (c & c)' [1.0/1.0] 1.0
t5t6i = (t51 & b & ci)' [1.5/1.5] 2.5
t0 = ai & di ===> t0i = a + d [2.0/2.0] 2.0
t4 = a & c & d ===> t4i = (a & c & d)' [1.5/1.5] 1.5
k = t0 + t4 + t5t6 =2=> k = (t0i & t4i & t5t6i)' [1.5/1.5] 4.0
==l==
t52 = b [xor] d [2.0/2.0] 2.0
t3t6 = t52 & ci ===> t3t6i = (t52 & ci)' [1.0/1.0] 3.0
t2 = ai & c =1=> t2i = a + ci [2.0/2.0] 3.0
ai = a' =2=> ai = (a & a)' [1.0/1.0] 1.0
t2i = (ai & c)' [1.0/1.0] 2.0
['l' jaoks on mõlemad variandid võrdsed nii pindala kui ka viite poolest]
['m' jaoks on viite poolest parem teine variant]
l = t2 + t3t6 ===> l = (t2i & t3t6i)' [1.0/1.0] 4.0
==m==
t53 = a & bi ===> t53i = (a & bi)' [1.0/1.0] 1.0
t54 = t2 + t53 ===> t54 = (t2i & t53i)' [1.0/1.0] 3.0
di = d' ===> di = (d & d)' [1.0/1.0] 1.0
t1t8 = di & t54 ===> t1t8i = (di & t54)' [1.0/1.0] 4.0
t6 = b & ci & di ===> t6x = (c + d)' [1.5/1.5] 1.5
t6i = (b & t6x)' [1.0/1.0] 2.5
t7 = b & d ===> t7i = (b & d)' [1.0/1.0] 1.0
m = t1t8 + t6 + t7 ===> m = (t1t8i & t6i & t7i)' [1.5/1.5] 5.5
==n==
bi = b' ===> bi= (b & b)' [1.0/1.0] 1.0 t9 = bi & c ===> t9i = (bi & c)' [1.0/1.0] 2.0 n = t1t8 + t4 + t9 ===> n = (t1t8i & t4i & t9i)' [1.5/1.5] 5.5
Aluseks vahevariant #2.
ai = (a & a)' [1.0/1.0] 1.0 bi = (b & b)' [1.0/1.0] 1.0 ci = (c & c)' [1.0/1.0] 1.0 di = (d & d)' [1.0/1.0] 1.0 t0i = a + d [2.0/2.0] 2.0 t2i = (ai & c)' [1.0/1.0] 2.0 t4i = (a & c & d)' [1.5/1.5] 1.5 t6x = (c + d)' [1.5/1.5] 1.5 t6i = (b & t6x)' [1.0/1.0] 2.5 t7i = (b & d)' [1.0/1.0] 1.0 t9i = (bi & c)' [1.0/1.0] 2.0 t51 = (a & d)' [1.0/1.0] 1.0 t52 = b [xor] d [2.0/2.0] 2.0 t53i = (a & bi)' [1.0/1.0] 1.0 t54 = (t2i & t53i)' [1.0/1.0] 3.0 t1t8i = (di & t54)' [1.0/1.0] 4.0 t3t6i = (t52 & ci)' [1.0/1.0] 3.0 t5t6i = (t51 & b & ci)' [1.5/1.5] 2.5 k = (t0i & t4i & t5t6i)' [1.5/1.5] 4.0 l = (t2i & t3t6i)' [1.0/1.0] 4.0 m = (t1t8i & t6i & t7i)' [1.5/1.5] 5.5 n = (t1t8i & t4i & t9i)' [1.5/1.5] 5.5
Elemendid: 14 x 2-NAND, 5 x 3-NAND, 1 x 2-NOR, 1 x 2-OR, 1 x 2-XOR
Kokku: 22 elementi (+4.8% esialgsega võrreldes), suurus 27.0 (-40%), kriitiline tee 5.5 (-35%).
Üks kontrolli võimalus on simuleerimine VHDL abil (vt. koodi). Simulatsiooni tulemusena saadud lainekujudel vrdl. signaale k0 ja k2, l0 ja l2, m0 ja m2 ning n0 ja n2 (x0 on enne ja x2 pärast optimeerimist). Signaalid k_err, l_err, m_err ja n_err on kasutusel automaatseks võrdlemiseks. Üksikud pulsid pole vead, vaid on põhjustatud signaalide hilistumisest loogikalülides (nn. delta-viide). Esitatud lihtsa kontrolli puuduseks on see, et ei ole võrreldud tulemusi tõeväärtustabeliga, st. lähteülesandega, vaid 1. ja 2. punkti tulemusi omavahel.
Kui simulatsioonide tulemused ei klapi, tuleks viga üles otsida. Silumisnäidis annab ehk ettekujutuse, kuidas seda teha...
Oluliselt põhjalikum simuleerimine, kus võrreldakse 1. ja 2. punkti tulemusi lähteülesandega koos lihtsa simulaatori kasutamise õpetusega, leiab siit.
Ajaliselt täpsema mudeli saab, kui tuua sisse hilistumised loogikaelementides vastavalt ülesande tingimustele. Näidis-mudel koosneb kahest osast - testkeskkond ja skeem loogikaelementidel. Loomulikult on vaja ka loogikaelementide mudeleid. Simulatsiooni tulemusel on selgelt näha signaalide k2, l2, m2 ja n2 hilistumise võrreldes ideaalse juhuga (k0, l0, m0 ja n0).
Info simulaatorite kohta asub uuema näidislahenduse lehel.